Evolving Team Structure

This model is drawn from reft:ethiraj_bounded_2004¹, which is a stochastic evolutionary program (blind variation and selective retention). After replicating their model, we add cognitive elements and then frame it as a problem of team negotiation rather than blind search.

Model

The model consists of a single team $T$ (i.e. an engineering design team) with $K$ designer agents: $T = \{D_1, D_2,\ldots,D_K\}$ . As a whole the team must make $N$ design decisions, where each decision $a_i$ is a binary choice (for simplicity), thus the team’s decisions are represented by a binary vector $A = \{a_1, a_2, a_3, \ldots , a_N\}$ . Each designer agent is initially assigned $n$ design decisions, where $n = N / K$ .

Decisions and Dependencies

Design decisions sometimes depend on each other, either one-way or two-way (mutual). (We model dependencies as a As state of Nature.) For each decision, there is a vector of other decisions on which it depends, denoted with a prime: $a^\prime_i = \{a_x, a_y, \ldots, a_z\}$ where $x, y, z \in [1,N]$ and $\neq i$ . The overall structure of dependency can be represented as a Design Dependency Matrix refp:clarkson_predicting_2004, where an X in any cell denotes that the column element is dependent on the row element (e.g. in Figure 1a, $b_2$ is dependent on $a_1$ , but not the reverse). Two-way (mutual) dependence is denoted by X’s in corresponding cells above and below the diagonal (Figure 1b and 1d).

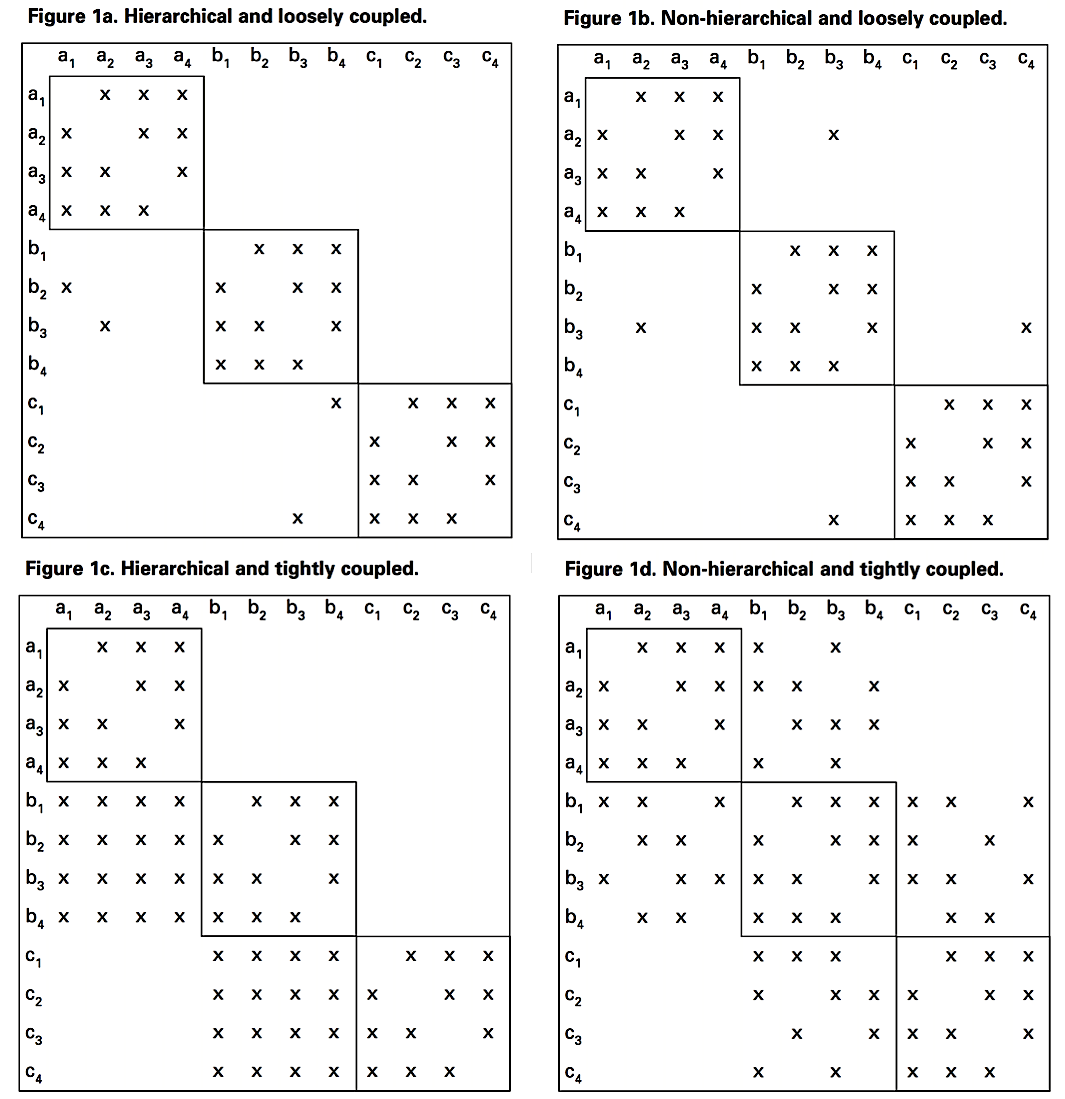
Figure 1. Examples of Design Dependency Matrices with four different structure types. In these examples, the team consists of three agents: A, B, and C, and each is responsible for four decisions. (*source*: Ethiraj and Levinthal, 2004)

Performance (a.k.a. fitness)

Each decision $a_i$ contributes toward the performance of the design as a function of its choice value (0 or 1) and the chocie values of its dependent decisions, which is the vector $a^\prime_i$ . This performance function $\omega_i$ contributes both to the individual designer agent $D_j$ who is responsible for that decision and to the overall team. Following refp:ethiraj_bounded_2004, we assume that performance contributions are uncorrelated and are a state of Nature, and therefore the function is a random draw from a uniform distribution $U(0,1)$ for all combinations of possible choice values.

$a^\prime_i = \{ a_x, a_y,\ldots, a_z\}; x, y, \ldots,z \in \{1,\ldots,N\}^{\neg i}$

$(a_i, a^\prime_i)\in\{(0,0,0,\ldots,0),(0,0,0,\ldots,1),\ldots$ $,(1,1,1,\ldots,1)\}$

$\omega_i(a_i, a^\prime_i) = U(0,1)$ $\omega_i = \cup f(a_i, a^\prime_i)$

For example, assume $a_i$ is dependent on three other decisions. There will be $2^4=16$ possible combinations of choice values, and therefore $\omega_i$ will be a vector of sixteen random draws $U(0,1)$ , one each corresponding to each combination: $\omega_i =$ (0.241, 0.640, 0.911, 0.153, 0.378, 0.107, 0.462, 0.887, 0.224, 0.621, 0.237, 0.081, 0.451, 0.715, 0.811, 0.499). All $\omega_i$ are set at initialization prior to a simulation run, and therefore calculating this function during a run is performed as a table lookup.

Following refp:ethiraj_bounded_2004, overall team performance function is the average of the performance contribution of individual decisions, given the current choice values in $A$ . All decisions have equal weight.

(Note: Other performance functions should be tested, including sum: "total effort", max: "best effort", and min: "weakest link".)

$\Omega(A) = \frac{1}{N} \sum_{i=1}^N{\omega_i(a_i, a^\prime_i)}$

Search, Adaptation, and Learning

During a single simulation run, each designer agent searches for better choice values using a random hill climbing technique (reft:ethiraj_bounded_2004 call this “first-order adaptation”, but we’ll call this “design adaptation” because it can be viewed as part of the design process). Each time step, a desiger agent $D$ randomly selects one of their $n$ decisions $a_i; i \in \{1,\ldots, n\}$ with uniform probability. ( $i$ and $k$ index decisions for $D$ , not the whole team, as above.)The choice value of $a_i$ is “flipped” to $\neg a_i$ , and is retained if the average performance for that agent improves:

$a_i \leftarrow \left\{ \begin{array}{ll} \neg a_i : \frac{1}{n}\sum_{k=1}^n{\omega_k(\neg a_k,a^\prime_k ) } > \frac{1}{n}\sum_{k=1}^n{ \omega_k(a_k,a^\prime_k )} \\ \\ a_i : \text{otherwise} \end{array} \right.$

At the team level, this search and adaptation process is not necessarily monotonic toward improvement because the choices of one designer can easily reverse the benefits choices made by other designers. Indeed reft:ethiraj_bounded_2004 included comments that many individual runs exhibited a significant degree of non-monotonicity.

In the simplest version of the model refp:ethiraj_bounded_2004 (“Version 1”), there is no learning by designer agents, and the team as a whole only learns to the extent that each designer has adjusted their decision choices to some equilibrium state (perhaps a local or global optimum).

Also, in Version 1 all designer agents have equal capabilities, in the sense that none are better than others in making any given set of decisions.

reft:ethiraj_bounded_2004 have another adaptation mechanism they call “second-order adaption”, but we will call “organizational adaptation” because it shifts the roles and responsibilities of designer agents, thereby changing their decision sets. We’ll explain this in “Version 2”, below.

Version 1: Design Adaptation Only

This model implements “Level One” adaptation in reft:ethiraj_bounded_2004 (described above). Each step, every agent randomly picks one of their decisions to flip, and keeps the result of the agent’s individual performance improves.

Try varying the two boolean experimental variables – “hierarchical” and “tightlyCoupled” and notice the results.


// Global parameters:
var N = 30;  // number of team decisions; Best to keep this below 40 to avoid excess run times
var K = 5;   // number of designer agents ("agents")
var n = Math.round(N / K);  // number of decisions assigned to each agent
// Experimental variables:
var hierarchical = true;
var tightlyCoupled = true;

var lambda = 4; // rate in poisson distribution that generates random dependencies

// Helper functions:
// binaryFlip(); arrayGet(arr,index); removeDups(arr); convertBinaryToInt(arr);
// flatten1(); pickN();
///fold:
//###########################################
var binaryFlip = function(){return flip() ? 1 : 0;}

// The following is necessary because of WebPPL's rule against using 
// Javascript libraries within WebPPL functions
var power = function(x,y) {return Math.pow(x,y);}

// Array get by index number
var arrayGet = function(arr,index){
return arr[index];
}

var arrayConcat= function(arrA, arrB){
return Array.prototype.concat(arrA,arrB);
}

var arrayLen = function(arr){
return arr.length;
}

// pick k unique random elements from an array
//  This is a recursive function, with safety counter
var addUniqueRandomElement = function(arr,k,acc,count){
if (count <= 0 || acc.length < k){
var x = sample(RandomInteger({n:arr.length}));
var newAcc = isIn(x,acc) ? acc : acc.concat(x);
var newCount = count - 1;
addUniqueRandomElement(arr,k,newAcc,newCount);
} else {
return acc;
}
}

var pickN = function(arr,k){
if (arr.length == 0){
return [ ];
} else {
var indexes = addUniqueRandomElement(arr,k,[],20);
return map(function(y){return arr[y];},indexes);
}
}

var isIn = function(y,arr){
if (arr.length > 0){
return any(function(x) { return x === y; }, arr);
} else {
return false;
}
}

var flatten1 = function(arr){
return reduce(function(x,acc){return Array.prototype.concat(x,acc);},[],arr);
}

// Remove duplicates from a sorted array
var removeDups = function(arr){
var dedup = reduce(function(z,acc){return isIn(z,acc) ? acc : [z].concat(acc); },[],arr);
return dedup;
}

// convert a binary array into an integer, for indexing purposes mainly
//  The focal decision should always be the last in the array
var convertBinaryToInt = function(arr){
var n = arr.length;
if (n > 0){
// (n - x - 1) is necessary because mapIndexed scans from left to right, rather than right to left
var decimalConversion = mapIndexed(function(x,y){return power(2,(n - x - 1)) * y;},arr);
var result = reduce(function(x, acc) {return x + acc; }, 0, 
decimalConversion);                                        
return result;
} else return 0;
}
///

//Agent and Decision functions
///fold:
//###########################################
// Agent functions for exploring decision alternatives
var invert = function(val){return val == 1 ? 0 : 1;}

// Takes an Array of decisions (binary), and inverts the element at the index
// returning a new array
var invertDecision = function(arr,i){
var result = mapIndexed(function(x,y){return x == i ? invert(y) : y;}, arr);
return result;
}

//###########################################
// Team decision variables
// A is the array of team decisions, randomly initialized.
var A = mapN(binaryFlip,N);

// This is an arrays of indexes for the Team as a whole
// Useful for functions that operate on the decision array A
var teamDecisionIndexes = mapN(function(x) {return x;},N);

//###########################################
// An Agent consists of a map that holds current state: 
//          1. decisions (indexes)
var createAgent = function(start, count){
var dIndexes = mapN(function(x){return x + start;},count);
return {decisions : dIndexes};
}


// Initialize an array of K agents
var agents = mapN(function(x) {return createAgent(x * n,n);},K);
//###########################################
// Create an array of arrays, each with a random list of dependent decisions (indexes)
var generateRandomDependencies = function (x) {
var count1 = sample(Poisson({mu:lambda}));
var count = Math.min(n,count1);
var otherDecisions = remove(x,mapN(function(x) {return x;},N)); // remove self
var len = otherDecisions.length - 1;
var result = sort(mapN(function(y){return otherDecisions[sample(RandomInteger({n:len}))];},count));
return removeDups(result);
}

//hierarchical && // add one-way dependencies, to higher-numbered agents
//      tightlyCoupled ? 
// all decisions between agents are dependent

// These dependencies match those in Ethiraj and Levinthal (2004)
var generateOtherDependencies = function() {
// for loose coupling, there are only two decisions with dependencies per Agent
var decisionsWithDependencies = 
flatten1(map(function(x){return pickN(x.decisions,2);}, agents) );
return mapN(function(x){
var m = n;
var startIndex = Math.round(x / m - 0.5) * m;
var agentIndex = Math.round(x / m - 0.5);
var result = x < (N - m) ? 
mapN(function(a){return (startIndex + m) + (a % m);},m)
: [ ];
var theseLooseDependencies = isIn(x,decisionsWithDependencies) 
? pickN(result,1) : [];
var result2 = tightlyCoupled ? result : theseLooseDependencies;
return result2;
}, N);
}

var otherDependencies = generateOtherDependencies();

var generateAgentDependencies = function(){
// this sets up mutual dependencies for all decisions with a single agent
var intraAgent = mapN(function(x){
var agentIndex = Math.round(x / n - 0.5) * n;
return remove(x, mapN(function(y){return agentIndex + (y % n) ;} ,n) );
}, N);
return intraAgent;
}

var combineAllDependencies = function(agentD,otherD){
return mapIndexed(function(j,k){
var arrB = otherD[j];
return arrayConcat(k,arrB);}
,agentD); //
}

// Array of arrays which list decision dependencies (indexes)
var randomDependencies = map(function(x){return generateRandomDependencies(x);},teamDecisionIndexes);

var dependenciesA = generateAgentDependencies();//randomDependencies;//

var dependencies = combineAllDependencies(dependenciesA,otherDependencies);

// Array of the counts of number of dependencies for each decision
var dependenciesCounts = map(function(x){return arrayLen(x) > 0 ? arrayLen(x) : 0;},dependencies);

// Array of the number of choice values needed for each decision, given the combinations 
//  of possible choise values for the focal decision and all its dependent decisions
var valueCounts = map(function(x){
return Math.pow(2,1 + x);}, dependenciesCounts);

// For focal decision d, return an array of its dependent choice values, plus itself

var getChoiceValues = function(decisions,d){
var focalDependencies = dependencies[d];
var dependentChoices = map(function(x){return decisions[x];},focalDependencies);
return dependentChoices.concat(decisions[d]);
}
///

//###########################################
// Performance calculations -- set once during initialization
///fold:
var performances = map(function(x) {
return mapN(function() {
return sample(Uniform({a:0,b:1}));
} ,x);
},valueCounts) ;

// Stub
var computeDecisionPerformance = function (decisions,i){
var choiceValue = convertBinaryToInt(getChoiceValues(decisions,i) );
var perfPossibilities = performances[i];
return perfPossibilities[choiceValue];
}

// Given current decisions for individual Agents and Team as a whole
var computePerformance = function(decisions,decisionIndexes){ 
var num = decisionIndexes.length;
var sum_performance = reduce(function(x, acc) {return computeDecisionPerformance(decisions,x) + acc; }, 0, decisionIndexes );
var max_performance = reduce(function(x, acc) {return computeDecisionPerformance(decisions,x) > acc ?  computeDecisionPerformance(decisions,x) : acc }, 0, decisionIndexes );
var min_performance = reduce(function(x, acc) {return computeDecisionPerformance(decisions,x) < acc ?  computeDecisionPerformance(decisions,x) : acc }, Infinity, decisionIndexes );
return  {sum_performance : sum_performance
, avg_performance: sum_performance / num
, max_performance: max_performance
, min_performance: min_performance
};
}
///

//###########################################
// Agent choice function. Choose the explored (inverted) decision set 
//   if its performance exceeds that of the original decision set
///fold:
var isImprovement = function(original,exploration, decisionIndexes){
return computePerformance(exploration,decisionIndexes).avg_performance > 
computePerformance(original,decisionIndexes).avg_performance ;
}

var explore = function(agent,currentStepDecisions,nextStepDecisions){
var i = n;
var index = sample(RandomInteger({n:i}));
var decisionToExplore = arrayGet(agent.decisions,index);
// test using currStepDecisions, unaffected by other agents this step
var proposedDecisions = invertDecision(currentStepDecisions,decisionToExplore);
return isImprovement(currentStepDecisions,proposedDecisions,agent.decisions)  
? invertDecision(nextStepDecisions,decisionToExplore) 
: nextStepDecisions;
}
///
//#############################################
// MAIN simulation function (recursive steps)

var step = function(count,a){
if (count <= 0){
return computePerformance(a,teamDecisionIndexes).avg_performance;
} else {
var nextA = reduce(function(x,acc) {return explore(x,a,acc);},a,agents);
return  [computePerformance(a,teamDecisionIndexes).avg_performance].concat(step(count - 1, nextA) );
}
}
// Run the simulation
var stepCount = 100;
var runCount = 1;
var results = step(stepCount,A);
// Print results
var tightCoupleVsLoose = tightlyCoupled ? "Tightly Coupled" : "Loosely Coupled";
var hierarchicalVsNonH = hierarchical ? "Hierarchical" : "Non-hierarchical";
print(hierarchicalVsNonH + " " + tightCoupleVsLoose + " Decisions");
print("N = " + N + "; K = " + K + "; n = " + n);
print ("Average number of dependencies = " + listMean(dependenciesCounts));
viz.line(mapN(function(t) {return t;},stepCount),results);

Version 2: Organization and Design Adaptation

UNDER CONSTRUCTION

To Do

Implement stochastic/adaptive organization change process from reft:ethiraj_bounded_2004.

End Notes

1. ↩ This model is drawn from reft:ethiraj_bounded_2004, but we substitute “designer agent” for “department” and “team” for “organization”. reft:ethiraj_bounded_2004 use a population evolution mechanism (i.e. blind variation followed by fitness-based selection refp:golberg_genetic_1989 refp:simonton_campbells_2011) to model the search and adaptation process, whereas we use agent conception, reasoning, and negotiation mechanisms.