Status: draft

Last modified: 2016-10-31

Foundations

The two biggest ideas in this chapter are in the last two sections:

“Affordances Provide Informational Resources”
“Institutions as Resources and Constraints in Affordances”

To get there, we first build up a model of interdependent tasks, performance, and agent capabilities. If I succeed in my role as author/tutor, at the end you will see affordances and institutions in a whole new way.

Interdependent Tasks

Following the model in Evolving Team Structure, we’ll model a set of tasks inside a project as a vector of binary decisions. The assumption here is that we could translate any coding of a realistic project into this expanded-but-primative coding. For example, let’s say the project is to design a doorway. Focusing only on the width of the opening, this decision for this variable is a continuous value, i.e. positive-but-constrained real number. But we could code it as a set of binary decisions by binning the values and coding it as an eight element vector $a$ of mutually exclusive decisions:

$a_1$ : 0 up to 0.5 meters
$a_2$ : 0.5 up to 0.7 m
$a_3$ : 0.7 up to 0.9144 m
$a_4$ : 0.9144 m (Standard door width in US = 36 inches)
$a_5$ : 0.9145 up to 1.2 m
$a_6$ : 1.2 up to 1.8288 m
$a_7$ : 1.8288 m (Double the standard width)
$a_8$ : over 1.8288 m

Notice that the binning is not uniform. In principle, any continuous variable can be encoded in any way. But in nearly all cases, the “right” encoding will be specific and relevant to the problem and situation at hand. There will be higher resolution near critical values, and less resolution farther away.

Because the elements of the decision vector $a$ are mutually exclusive, there are only eight possible values and $2^3 = 8$ , therefore we can recode this into a three-bit binary decision $o$ : $(o_1 , o_2 ,o_3)$ .

A similar binary encoding procedure can be applied to decisions about structure and architecture, and also decisions about decisions.

If we concatenate all the decision vectors together, we’ll get one long binary vector of length $N$ . For the base model, we’ll treat this vector as fixed and exogenous (i.e. not influenced by agents or their decisions).

Performance

The performance $p$ of any given design is the weighted sum (we assume) of contributions of individual decisions, accounting for interdependencies. Following the model in Evolving Team Structure, we can model dependency between decisions through a matrix – Design Dependency Matrix (DDM) refp:clarkson_predicting_2004. Interdependent performance is coded by assigning a performance value for all combinations of dependent decisions. Example, if decision $a_1$ is dependent on four others $a_2, a_3, b_3, c_1$ , then there are $2^5=32$ possible performance values for $a_1$ . While reft:ethiraj_bounded_2004 assume uncorrelated performance values (i.e. maximally rugged landscape), we’ll be more realistic and assume correlated performance for nearby decision choices.

Performance Landscapes

A key concern is the distribution of performance values. If there is a single peak and all other values smoothly transition from low to high, then the design process is pretty simple. This would be a “smooth landscape”.

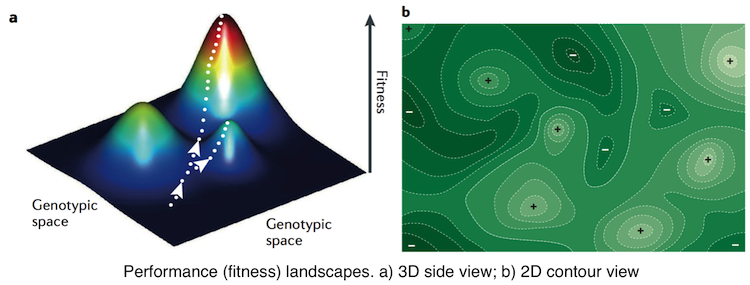
Conversely, if any point in the space is randomly and arbitrarily different from every other, then the landscape is maximally “rugged”. There can be no local notion of “making progress” or “improvement” – only is this point better/worse than that point.

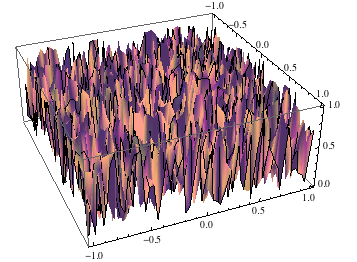A random performance landscape.

But ruggedness is not the only challenge of searching performance landscapes. For most complex designs there will be regions of infeasibility or impossibility where the design “falls apart” or “never comes together”. (Some surfaces can’t be painted. Some materials can’t be glued together. Two solid objects can’t occupy the same space at the same time.) These are “sink holes”, where once you get in them (by making design choices), it may be hard to get out of them through incremental changes. Here’s a nice diagram from reft:greenwood_use_1998 illustrating “sink holes” of infeasability.

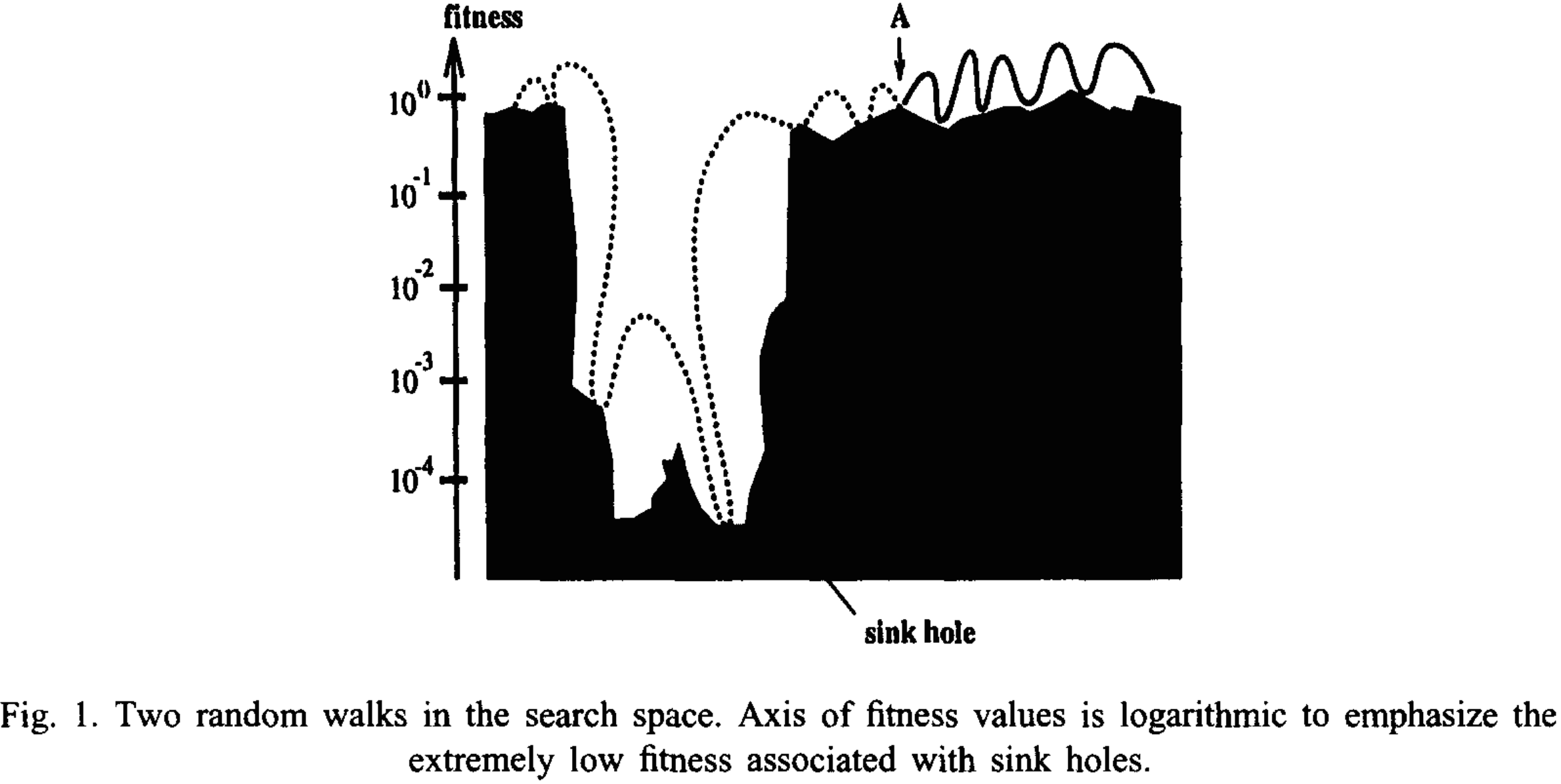
Following reft:greenwood_use_1998, we can define a metric of ruggedness $\mathscr{R}$ as “neighborhood correlation”. If we define a neighborhood of $m$ points within $d$ distance from a given point $x_0$ , then we can quantify ruggedness by the average correlation of performance from that point $p_0 = f(x_0)$ to the other points $x_1, x_2, \ldots x_m$ via some number of random walks. The ruggedness metric a set of “correlation lengths”, i.e. a correlation defined for each length (number of steps $s$ ) on the random walks (limited to the neighborhood around $x_0$ ):

$\mathscr{R}(s) = \frac{\langle p_i p_{i+s}\rangle - \langle p_i \rangle ^2}{\sigma_p^2}$

for every pair of performance values $s$ steps apart on the random walk, and where $\langle . \rangle$ is the mean of all values across a given random walk, and $\sigma_p^2$ is the standard deviation of $p$ values within that neighborhood. Constraint: anytime a random walk reaches a “sink hole”, it stops.

If we have a set of correlation lengths $\mathscr{R}(s)$ , and also a function to define regions of feasability, then we can randomly generate our performance landscapes. Let us assume that “islands” of feasability are surrounded by “oceans” of infeasability. Think of each “island” as a distinct architecture. We can adapt algorithms for generating random 2D “islands”. One such algorithm is “boundary of Brownian Motion”. (“Brownian motion” is a random path in space, while a “random walk” is the time series of random spatial points vs. time.). Here is an example, where “feasable” is the dark region.

A random fractal island

Agent Capabilities

Agents are endowed with a set of capabilites. A capability is a generalized ability to perform some function or achieve some goal to some degree of excellence. In the model in Affordances as Probabilistic Interrelations, the agent had a capability to estimate a distance span (e.g. doorway opening) relative to the agent’s body size and orientation. The realization of a capability always depends on the concrete details of context, especially the interaction processes with affordances.

Agents realize their capabilities by executing one or more routines (a.k.a. procedures, processes, actions). In this work, we won’t be concerned with the details of routines and therefore we will treat them abstractly. Learning by doing is the adaptive process of adjusting and refining routines based on experience.

To start with, we will assume that there is a fixed set of possible $n$ capabilities $C=c_1,c_2,\ldots,c_n$ , and each agent is randomly endowed with $k$ capabilities, $1 \leq k \leq n$ .

We’ll model three classes of capabilities: 1) Design capabilities – specific to classes of tasks; and 2) Reflection capabilites – observe and reflect on their actions and outcomes of their own and other agents; and 3) Interaction capabilities – basic protocols for discourse, conflict resolution, and decision-making.

Because we are abstracting the design process as the search for good or better design decisions, we’ll model capabilities as (abstract) alternative search strategies, whose effectiveness in any situation is governed my the affordances associated with the design tasks.

Affordances as (Probabilistic) Interrelations

An affordance is an interrelation between an agent and its environment that serves as a resource for action, or facilitates action, given the agent’s capabilities, intentions, purposes, and attention. In other words, an “affordance” is not just a signal (i.e. sensory data) or an interface or a protocol for action. Instead it is a resource for action, both before, during, and after task execution.

We treat affordances as probabilistic interrelations because they are governed by uncertainty and randomness, including the perception and reasoning processes of agents as they engage with them. (See: Affordances as Probabilistic Interrelations).

In most of the literature on affordances, the focus is on an agent in a physical environment, and perception-action processes. reft:rietveld_rich_2014 assert that the construct of affordance extends much further, including nearly all of human social life. In that spirit, we use affordance to model the fit between agents and task sets.

Agent-Task Fit as Affordance

What does it mean when a team member (agent) is a “good fit” for a set of tasks? It means that that agent has a set of capabilities that are well-matched to the nature of the tasks, and when they are skillfully applied, that the outcome will be good/positive/as required.

Agents perform tasks by engaging with them. They start with a general approach and disposition, assess the particulars of the task, and then take steps (actions, decisions, etc.), and check along the way whether they have reached their goal or other stopping condition. Not everything is worked out in advance or at the start. The particulars of each step in the process can bring forward, in the expert, a large set of possibilites and insights that guide further action.

In a sense, affordances are the interface between the generality of an agent’s capabilities and the concrete requirements and constraints of specific tasks (or, more generally, action settings). But it’s more than an interface, which might be modeled simply as a translation or interpretation process (e.g. converting AC to DC current in electrical circuits). It’s also more than a communication protocol, which is “a system of [codes and] rules that allow two or more entities of a communications system to transmit information” (Wikipedia). As mentioned in the previous section, affordances serve as resources to agents with adequate capabilities.

Affordances Provide Informational Resources

There are four^* general classes of informational resources that affordances provide. The first is information about progress. As the agent engages in a task, it often needs to gauge progress, either toward a goal, or toward completion, or diminishing returns on effort, or even just some “getting warmer…getting colder…” indications. This is vital in complex combinatorial problems in order to identify and “save” good intermediate results (“building blocks”). Without this, agents would need to complete all steps in a task before assessing performance (if they can), and then start over to search for an improvement. This is a factor of 10, 100, or thousands of times slower, depending on the size of the search space.

^*Four classes that a I can think of right now. There could easily be more.

The second class of informational resources are conditional alternatives. This is best explained in the context of artistic improvisation (musical, acting, etc.). The actions and choices each artist builds on what has come before and what is unfolding at each moment. While the unfolding could, in principle, be linear and unsurprising, the art of improvisation comes forward whenever the artists take new and unexpected directions, often in the face of apparent impasses – “how will they get out of this?”. Exception conditions – deadends, faults, mistakes, silences – don’t bring a halt to the performance, but instead artists draw on a set of conditional alteratives in what has come before, and from their experience generally.

Likewise, designers enaged in a set of design tasks may face exception conditions that require on-the-fly changes to plans, approach, disposition, methods, and so on. In these cases, a human designer doesn’t “crash” like a computer program might, but instead they improvise. It is their on-going engagement with the task as affordance that allows them to create/see the alternatives that might allow them to move forward.

The third class of informational resources are framing signs. “Framing” is the cognitive process of making sense of a situation and then adopting an appropriate cognitive disposition to fit the situation. In any sort of rich open environment, agents need to constantly answer “What sort of situation am I in? What sort of problem is this? What is important to see/know/attend to, and what is unimportant?” The Frame Problem arises, as reft:felin_economic_2014 argue, because that number of uses of anything (say, the forms and functions of a screwdriver in all possible use cases and activities) are both indefinite and unorderable. In non-ergotic systems, there is no full account or set of algorithms that can be given about all possible actions, uses, and functions:

“The frame problem focuses us on the problematic nature of explaining the full task set of activities and possible functionalities and uses for operating in the world (or some situation or environment, whether real or artificial).” (reft:felin_economic_2014, p 5)

But humans and other intelligent agents solve the “Framing Problem” all the time, at least to an adequate degree. How? But not relying solely on ex ante reasoning and conceptualization. Instead they engage with their affordances to tease out the framing that is suitable.

I call these resources “framing signs” in order to invoke the field of Semiotics (esp. Peirce’s Theory of Signs as a method and approach to understand signs as three inter-related parts: a sign (“sign-vehicle”), an object, and an interpretant (the agent).

For designers starting any set of tasks, they will begin with some frame about the nature of the task, what the action process will look like, what they might experience along the way, and what “completion” looks like. But whatever framing they start with will be subject to testing and validation all along the way. The designer’s frame helps set expectations, and the fulfillment or failure of expectations create information for the designer that either confirm or refute the current frame. The difference between novices and experts is often in the sophistication of their mental frames, and also in how frames will be modified or replaced as circumstances change.

Institutions as Resources and Constraints in Affordances

The fourth (and final^*) class of informational resources provided by affordances are institutions. Another way of saying this is that, to a certain extent, institutions are embedded in affordances. Institutions are norms and rules that govern social interaction, organization, identity, and behavior. Most sociologists and economists construe institutions within a framework of individual incentives, rational utility maximization, and especially punative social processes/mechanisms when norms and rules are violated.

^*For now.

Taking a cognitive turn¹, we will construe institutions differently. Institutions are part of the way people think, embedded in mental frames, in behavioral dispositions, and (crucially) in affordances. “It’s just how things work.” In contrast to the traditional view on institutions, most of the time most people are not thinking about all the possible negative consequences of violating norms and rules, and weighing them against the possible benefits of violations. This is especially true for people who are inculturated in those norms and rules. They are pro-social because it has become a part of their thinking, not because of cost/benefit analysis.

Institutions, as resources and constraints, have several affects on agents and their interrelations with affordances. First, they reduce uncertainty and ambiguity for agents, especially regarding cause-effect relationships, exception handling, and relevant information (including signs). Second, institutions provide alternatives and constraints. Essentially, agents can call upon these alternatives or constraints when the need arises, without knowing or planning everything in advance. Finally, institutions greatly facilitate both codification and abstraction of social behavior, and conversely institutions are frequently realized through codified and abstracted information and knowledge.

Teams, whether formal or informal, are constituted and sustained through institutions. Otherwise, they are merely accidental or emergent social phenomena. Examples include authority, governance, power (i.e. control over resources, opportunity, or other people) dispute resolution, rewards and sanctions, autonomy, collaboration, affiliation, and member identity.

Coding Institutions

This institutional phenomena just listed may appear to some readers to be a squishy mess, and therefore very hard to codify in computer programs or other formal systems. Luckily, Elinor Ostrom and her colleagues devised a “Grammar^* of Institutions” refp:ostrom_grammar_2009 that are well suited to our purposes.

^*It is not a really grammar in the usual sense: production rules over terminal and nonterminal symbols. It is more like a nested set of templates or patterns. Even so, we will use the original label.

The components of the grammar are identifed using the acronym ADICO, which stands for:

Attributes – the characteristics of agents to which the institution applies, including existental qualifiers “at least one” or “some” (∃) and “all” (∀)
Deonic – a modal operation $D \in \{P,O,F\} =$ Permitted, Obliged, and Forbidden.
AIm – the actions or routines that are invoked (or forbidden) by the instituion
Conditions – characteristics of the situation define when and where the insitution applies
Or else – consequences to the agents for noncompliance

Part of what makes these a “grammar” is that they can be taken in subsets to codify three different manifestations (statement types) of institutions:

Statement type	Acronym	Elements
1. Shared moves (strategies)	AIC	[ATTRIBUTES][AIM][CONDITION]
2. Norms	ADIC	[ATTRIBUTES][DEONIC][AIM][CONDITION]
3. Regulative rules	ADICO	[ATTRIBUTES][DEONIC][AIM][CONDITION][OR ELSE]

Shared Moves

Shared moves^* are choices, decisions, or courses of action relating to some function. “Shared” means that they are held in common among a social group of agents, through language, stories, folk theories, and expectations.

^*a.k.a. "strategies" in Game Theory. While Ostrom and most others use "strategy", I prefer "move" so that we can reserve "strategy" for usage in the sense of "management strategy" or "military strategy".

Notice how the coding of Shared Moves map nicely to the Beliefs-Desires-Intentions (BDI) formalism for specifing reactive agent behavior rules. “Beliefs” are the conditions that need to be true in order to trigger the behavior. “Desires” are the end goals or terminating conditions for the behavior. “Intentions” are the actions that constitute the behavior (a.k.a routines in the ontology of Functional Ecosystems).

[ATTRIBUTES] ↔︎ « qualifying characteristics of agents »
[AIM] ↔︎ Intentions and Desires
[CONDITION] ↔︎ Beliefs

There is an important difference, however. Shared moves are “in” the affordance, while BDI are “in” individual agents. Viewed as a computational system, we can say that “[AIM] invokes the matching Intentions and Desires” in a given agent that has matching qualifying characteristics ([ATTRIBUTES]), and vice versa. Likewise, we can say that “[CONDITION] invokes the matching Beliefs”in a given agent that has matching qualifying characteristics ([ATTRIBUTES]). The difference from ordinary BDI agents is that our agents carry out behaviors by “plugging into” the relevant/matching affordances through out the process, whereas BDI agents do it all on their own, including sensing the state of their envionment to match against Beliefs.

Shared moves are the most volitional. Given the specifics of any situation, an agent might or might not choose to execute any of the relevant shared moves. We can think of them as common “tendencies”, “defaults”, “priors”, or (in some cases) “habits”. In terms of social cognition, the effect of shared moves is reduced cognitive load on any individual agent because they have ready access to what other agents are most likely to do in common situations.

Norms

Norms are shared moves that also have a prescriptive or nonprescriptive element: “can”/”may”; “should”/”must”; or “should not”/”must not”. They also convey what (agents collectively believe) is physically or ontologically possible, if that is germane to the institution.

Rules

Rules are norms that have punishments, penalties, sanctions, or other negative consequences on agents who violate the rule. This means more than a raised eyebrow or disapproving scoff. Agents are assigned a social identity of “violator”, at least for a period of time. The [OR ELSE] actions specify the methods and procedures for carrying out the negative consequences, which may be physical, material, status/role, or negative social interaction (“shunning”). Implied in this codification is that there are some social processes or mechanisms to carrry out the [OR ELSE] actions. Because they can be any combination of moves/actions, norms, and rules, we model the enforcement institutions in a social group using the same ADICO grammar. For example, for an employee of a company who leaks company secrets, the [OR ELSE] consequence might be “the violator loses his job”, which would invoke a matching set of shared moves, norms, and rules by that employee’s manager, the HR department, the Legal department, and so on.

reft:ostrom_grammar_2009 chose to model norms in a way that fits Game Theory and rational expectations calculations by agents regarding subjective payoffs (utility). She defines “delta parameters” that add or subtract a fixed amount or percentage from the expected payoffs from the relevant moves or actions: add $\delta_o$ for obeying a prescription and subtract $\delta_b$ for breaking it, with $\Delta = \delta_o + \delta_b$ . Ostrom further subdivides the deltas into “internal” and “external” depending on the “source”, i.e intrinsic vs. extrinsic incentives.

A New Modeling Approach

☞ Here’s where things get interesting and we part company with reft:ostrom_grammar_2009 and also BDI agent modelers.

We will implement norms through affordance interrelations that directly shape what agents can and can’t do, and what they (feel) compelled to do nor not do. This is a much more direct way to model norms, it is more cognitively and behaviorally plausible, and has nice characteristics in open/evolving environments that we care about.

Any norm that has a “can/may” deonic (or “cannot/may not”) will have [AIMs] and/or [CONDITIONs] added (or taken away), thus increasing (or decreasing) the available/possible Intentions, Desires, and Beliefs that will be invoked when a given agent engages with that affordance.

Example

To illustrate, here is an example. Let’s say a design team has a norm that specifies that “Any designer MAY make a change to any other designer’s decisions at any time.” We’ll call this affordance “Changable”^*. The [ATTRIBUTES] for this norm would be “any designer” (subject of the action) and “any decision (regardless of owner)” for the object of the action. The [AIMs] would include any design change that a given is designer is capable of making. The [CONDITION] would be “any time”.

^*I think clarifies if we label affordances with action terms ending in "-able".

This affordance is engaged when a given designer wants to make some change (pre-specified or not) to some decision (pre-specified or not). In the course of engaging, a specific change and decision are identified, which enables the [AIMs] to be carried out, which in turn involves invoking that agent’s capabilities and associated routines.

Flip our example norm around. Say the norm is “ONLY the designer who owns a decision MAY make a change to that decisions at any time.” Replay the sequence we just walked through, where some other agent (not the owner) tries to make a change. That agent no longer matches the [ATTRIBUTES], and therefore that agent will no longer have the informational resources provided by the affordance to carry out the change. The agent, being purposeful and volitional, might still try to make the change, but their likelihood of succeeding will be much lower – purely due to the extra cogntive and behavioral load of working outside of the norm (including increased uncertainty) and also the reduced probability of good outcomes, the increased probability of bad/undesirable outcomes.

This last point is very important.

As I said when I introduced institutions, the way they work (mostly) is by providing informational resources that make life easier for agents (so to speak). If you conform to the norms of your social group, your thinking and actions effectively “stand on the shoulders” of the collective cognitive and behavioral resources of the group. If you choose not to conform to the norms, then you are going alone.

In our affordance-based modeling approach, we don’t need to invent bonus and penalty parameters for agent utility functions. How would you do that in an open and evolving environment, anyway?

Back to the task of implementing norms through affordance interrelations, we can use similar mechanisms for “should/should not” and also “must/must not” deonics. In essense, these would be implemented as fuzzy match requirements (for “should/should not”) and hard match requirements (for “must/must not”). “Fuzziness” is simply “degree of match”, where the parameters of the fuzzy match logic are created through the combined agent-plus-affordance engagement.

How Institutions Become Part of Thinking/Seeing/Doing

So how do agents incorporate norms into their thinking (i.e. planning, reasoning, evaluating, etc.), perceiving, and behaiving? There are five possible ways:

They unknowingly violate a norm, and then reflect on their experience of the consequences.
They reason forward to estimate the probable outcomes of conforming to a norm, or not.
They observe other agents conforming (or not) to a norm, and reason about those outcomes.
They learn a norm through instruction or other social interaction (e.g. imitation)
They internalize a norm by shaping their own conception and behavior processes, effectively habituating the norm.

Not all agents will internalize norms (and rules) in all of these ways. Circumstances, capabilities, and past experience will determine how it happens.

The fifth way is very important, because this is the state of agents who are incultrated in the norm (or rule), and therefore the agents no longer consider any courses of action other than conforming to the norm (or rule). Sociologists see institutions as largely taken-for-granted, and not something that people in society constantly thinking about. Effectively: “This is just the way we do things.”

With these foundational ideas established, we are now in a position to begin modeling. (At long last!)

NEXT: The Model

Endnotes

1.↩ Late in their careers, both Douglas North and Elinor Ostram (Nobel Prize laureates in Economics) turned their attetion to the cognitive aspects of institutions. reft:north_economics_2010 posed the general question as "how human beings learn and meld beliefs and preferences to make the choices that underlie economic theory; and how and why they develop theories (and act on them) in the face of pure uncertainty". He believed the answers would come from a meld between economics, sociology, and cognitive science, and would lead to "major breakthroughs".